
DoE-Happen #55: Von OFAT zum echten Verständnis – wie gutes Design (DoE) einem Werkstudenten die Augen öffnete!
Heinz ist Werkstudent in einem mittelständischen Unternehmen der Polymerverarbeitung. Sein Auftrag klingt simpel: Ein 2K-Harz soll prozessseitig hinsichtlich Festigkeit und Verarbeitung optimiert werden. Zwei Faktoren stehen im Fokus: Rührgeschwindigkeit und Temperatur. Der Prozess soll effizienter und robuster werden – mit möglichst wenig Versuchen.
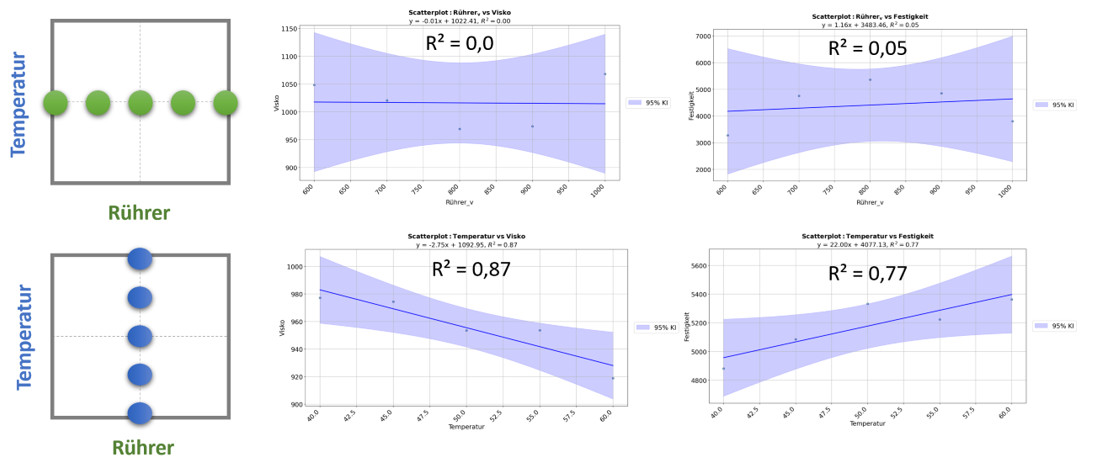
Abbildung 2: OFAT-Versuchsansatz – scheinbar systematisch, tatsächlich aber blind für Wechselwirkungen und Nichtlinearitäten. Die Einflüsse der Faktoren bleiben isoliert – komplexe Ursache-Wirkung-Zusammenhänge bleiben verborgen.
Heinz denkt: „Klingt machbar – zwei Faktoren, das sollte sich mit OFAT locker lösen lassen.“– One Factor At a Time.“
Heinz startet Versuchsreihen, bei denen jeweils ein Faktor verändert wird, während der andere konstant bleibt. Zuerst variiert er die Temperatur bei 800 U/min, danach die Rührgeschwindigkeit bei konstanten 42,5 °C. Er dokumentiert akribisch: Viskosität und Festigkeit des Endprodukts.
Anfangs scheint alles plausibel. Die Viskosität sinkt mit steigender Temperatur – erwartungsgemäß. Auch höhere Rührzahlen scheinen kurzfristig die Mischung zu verbessern. Doch dann häufen sich die Inkonsistenzen:
- Bei hoher Drehzahl sinkt die Reißfestigkeit.
- Manche Proben zeigen deutlich verringerte Festigkeit – trotz angenommener optimaler Viskosität.
- Blasenbildung tritt sporadisch auf.
Heinz beginnt zu zweifeln. Seine Ergebnisse widersprechen sich. Die Ursache bleibt unklar. Er landet im berüchtigten „Tal der Tränen“ – dem typischen Tiefpunkt schlecht geplanter Versuchskampagnen.
Die Wende – vom Rätselraten mit OFAT zur Struktur mit DoE
Mit jeder neuen Versuchsreihe wird die Situation frustrierender. Trotz vieler Wiederholungen bleibt das Verhalten des Systems unklar. Vor allem die Rührgeschwindigkeit scheint sich „seltsam“ zu verhalten: Bei mittleren Drehzahlen wirken die Proben gut durchmischt. Doch bei höherer Geschwindigkeit kippt das Ergebnis: Die Festigkeit sinkt, die Oberfläche wird poröser. Gleichzeitig treten Blasen auf – und dabei war doch die Annahme vom QM, dass etwas mit der Mischqualität nicht passen könnte.
Heinz dachte: Mehr hilft mehr! Dennoch beginnt er zu recherchieren – und stößt auf einen entscheidenden Hinweis:
Abbildung: „Übermäßige Scherung kann fragile Füllstoffe wie Aerosile beschädigen.“
Langsam beginnt er zu verstehen: Die Rührgeschwindigkeit entfaltet eine nichtlineare Wirkung. Bis zu einem gewissen Punkt hilft sie beim Dispergieren – danach jedoch beginnt sie, die Füllstoffstruktur zu schädigen. Eine klassische Überarbeitung durch übermäßige Scherkräfte.
Die Temperatur hingegen zeigt – wie erwartet – einen linearen Effekt: Je höher die Temperatur, desto niedriger die Viskosität – das unterstützt das Benetzen und die Homogenisierung des Systems. Und möglicherweise gibt es noch einen Effekt, den man bisher nicht isolieren konnte: eine Wechselwirkung zwischen Temperatur und Rührgeschwindigkeit – also eine Verstärkung oder Abschwächung in Abhängigkeit ihrer Kombination?
Doch wie lässt sich das belegen?
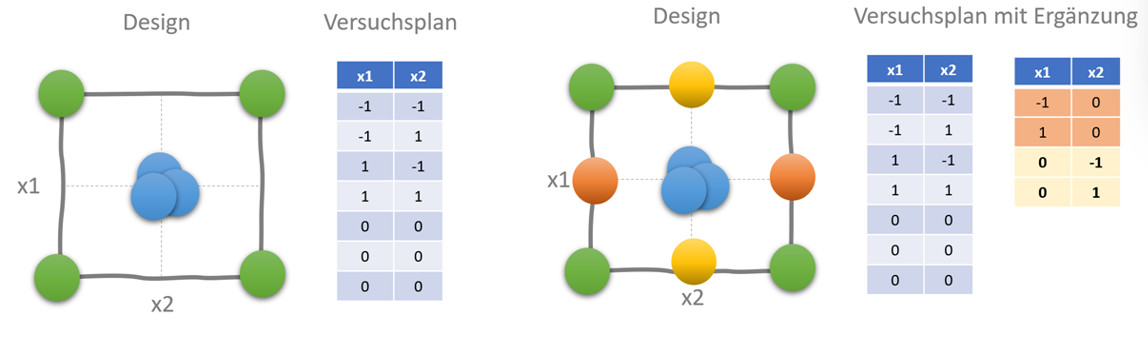
Abbildung 3: Übergang von OFAT zu einem CCF-Versuchsplan. Nur ein strukturierter Designansatz ermöglicht das gezielte Erkennen von Nichtlinearitäten und Wechselwirkungen im Prozess.
Statistik? Bitte nicht … oder doch?
Als Heinz mir von den Problemen erzählt, bekommt er einen simplen Rat:
„Warum machst du nicht einfach ein DoE?“
Heinz schluckt. Statistik? In der Firma löst das eher Sorgenfalten aus. „Viel zu kompliziert, wir brauchen schnelle Ergebnisse!“ – ein Satz, den man leider oft hört. Doch Heinz bleibt hartnäckig und setzt sich durch.
Er erstellt ein vollfaktorielles 2²-Design mit Centerpoints – ergänzt um gezielte Randpunkte, um insbesondere den nichtlinearen Einfluss der Rührgeschwindigkeit sowie potenzielle Wechselwirkungen sauber auflösen zu können. Damit nutzt er im Prinzip ein CCF-Design (Central Composite Face-centered) – ein kompakter Versuchsplan, der ihm erlaubt, mit wenigen gezielten Versuchen ein vollständiges Bild zu erzeugen.
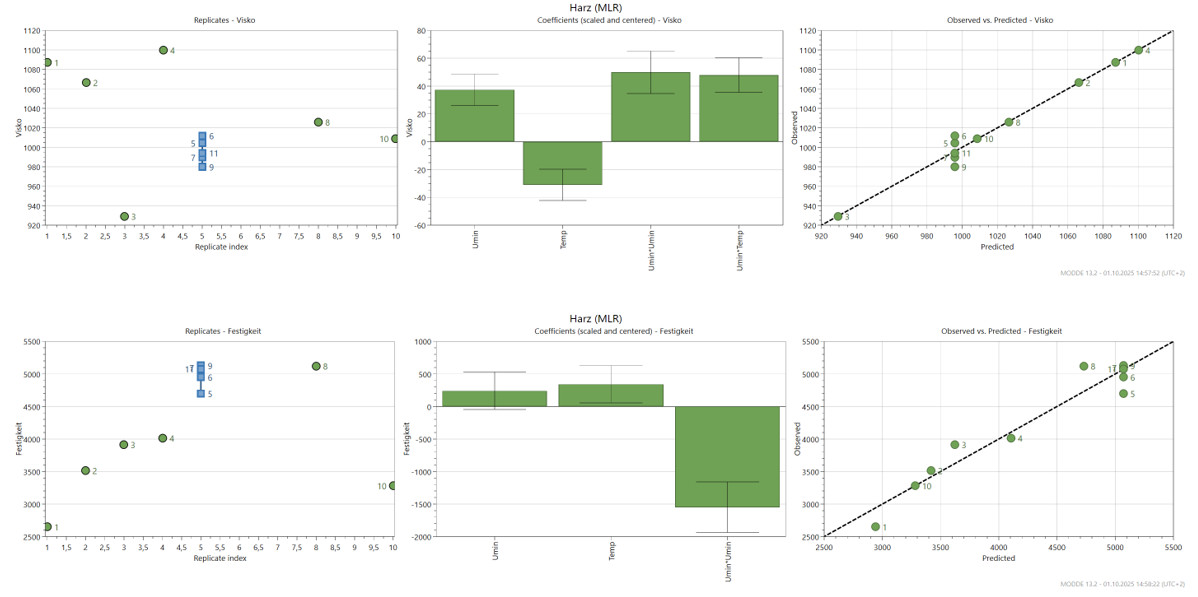
Abbildung 4: Darstellung beider Zielgrößen in „Replicate Plot“, „Koeffizienten Plot“ und „Observed vers Predicted Plot“ (SW: Modde)
Heinz startet die Auswertung seiner Daten – systematisch und fundiert. Dabei helfen ihm drei zentrale Plot-Typen:
- Replicate Plot (links) Abbildung 4
Der Replicate Plot zeigt, wie stark die Messergebnisse bei exakt gleichen Versuchsbedingungen streuen – in diesem Fall bei den mehrfach durchgeführten Centerpoint-Versuchen. (blau dargestellt)
Warum ist das wichtig?
In jedem Versuch gibt es natürliche Schwankungen: kleine Abweichungen in der Handhabung, Messungenauigkeiten oder Effekte, die sich nicht direkt kontrollieren lassen. Der Replicate Plot macht sichtbar, wie stark die Ergebnisse bei gleichen Bedingungen streuen – also wie verlässlich der Versuch bei Wiederholungen ist.
Je enger die Wiederholungen beieinanderliegen, desto zuverlässiger ist das Gesamtsystem. Denn dann ist klar:
Die Variation in den Zielgrößen (z. B. Festigkeit oder Viskosität) kommt tatsächlich durch die Veränderung der Faktoren – und nicht durch Zufall oder Messfehler.
Für Heinz ist das die erste wichtige Bestätigung:
Die Prozessdaten sind in den Center-Points stabil und reproduzierbar.
Das bedeutet: Er kann sich auf die weiterführenden statistischen Berechnungen verlassen – etwa für die Modellbildung, die Varianzaufklärung per ANOVA und die Signifikanzprüfung einzelner Effekte mithilfe von t-Tests..
- Koeffizienten Plot (Mitte) Abbildung 4:
In diesem Diagramm werden die Einflüsse der untersuchten Faktoren – also Temperatur und Rührgeschwindigkeit – auf die Zielgrößen grafisch dargestellt. Grundlage dafür ist ein Rechenmodell (eine sogenannte Regression), das zeigt, wie stark sich Veränderungen bei den Faktoren auf das Ergebnis auswirken.
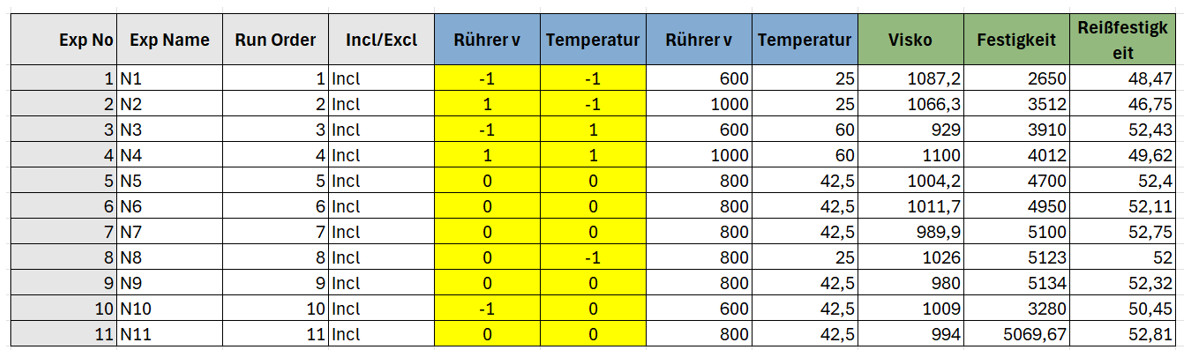
Abbildung 5: Darstellung des Versuchsplans mit codierten (gelb) und Original-Faktoreinstellungen
Um die Einflüsse direkt vergleichen zu können, wurden die Werte standardisiert – also auf eine gemeinsame Skala gebracht. Egal ob Temperatur in °C oder Rührgeschwindigkeit in U/min: Im Modell sind alle Faktoren gleich gewichtet – wie Äpfel und Birnen, die man plötzlich vergleichen kann. So spielt es keine Rolle mehr, ob ein Faktor ursprünglich in °C oder U/min gemessen wurde – alles ist auf einer gemeinsamen Skala vergleichbar.
Aber keine Sorge die Software (hier Modde) zeigt die wo sinnvoll alle Werte in Originaleinheiten an!
Der Plot zeigt:
- Haupteffekte → Wie stark wirkt jeder einzelne Faktor?
- Wechselwirkungen → Was passiert, wenn zwei Faktoren gleichzeitig verändert werden?
- Quadratische Anteile → gibt es eine nichtlineare Wirkung, z. B. eine optimale Rührgeschwindigkeit, nach der sich das Ergebnis wieder verschlechtert?
Das Entscheidende dabei:
Nicht nur die Richtung (plus/minus) wird sichtbar, sondern auch die Größe und Bedeutung der Effekte.
Mit Hilfe der Konfidenzintervalle (die Linien / Antennen an den Balken) erkennt man zudem, ob ein Effekt statistisch sicher ist – oder nur zufällig wirkt.
- Observed vs. Predicted Plot (Rechts) Abbildung 4:
Dieser Plot vergleicht, was wirklich im Versuch gemessen wurde (Observed), mit dem, was das Modell auf Basis der Versuchsplanung vorhergesagt hat (Predicted).
Man kann sich das so vorstellen:
Das Rechenmodell „sagt voraus“, wie hoch z. B. die Festigkeit bei einer bestimmten Kombination aus Temperatur und Rührgeschwindigkeit sein müsste. Anschließend wird überprüft, ob die tatsächlichen Versuchsergebnisse zu diesen Vorhersagen passen.
Jeder Punkt im Plot steht für einen Versuch.
Je näher die Punkte an der Diagonalen liegen, desto besser stimmt das Modell mit der Realität überein.
Und genau das ist bei Heinz der Fall: Die Punkte folgen eng der Linie – das heißt, sein Modell kann die Ergebnisse im untersuchten Bereich zuverlässig vorhersagen.
Doch worauf basiert dieses „Modell“?
Es beschreibt die Wirkung der Faktorvariation auf die Zielgrößen. Da im Design die beiden Faktoren unabhängig voneinander variiert wurden, sind auch ihre Effekte weitgehend entkoppelt (unabhängig) berechenbar.
Daraus ergibt sich nicht nur ein tragfähiges Ursache -Wirkung Regressionsmodell, sondern auch ein Vorhersagefehler, der quantifizierbar und visualisierbar ist.
Beispielsweise gelingt uns diese Visualisierung mit dem Main Effect Plot, der zusätzlich den Vertrauenskorridor abbildet. So lässt sich abschätzen, welche Ergebnisse zu erwarten sind, wenn wir eine bestimmte Faktorkonstellation im Versuch einstellen.
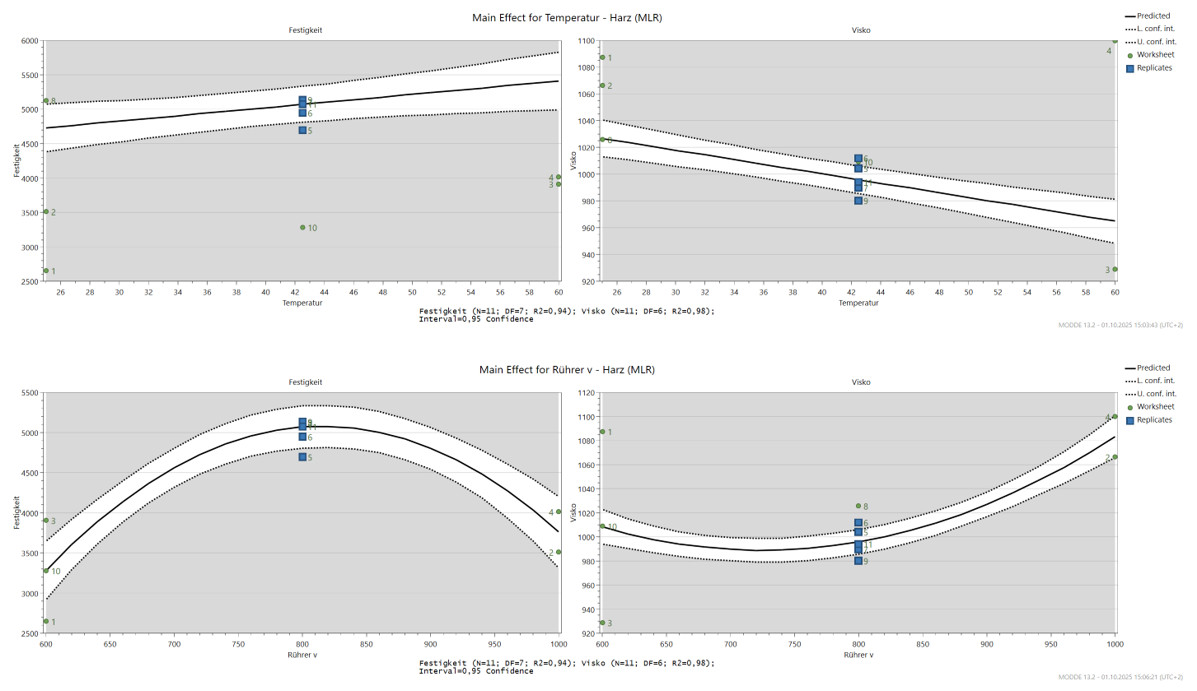
Abbildung 6: Modellbasierte Auswertung – Reproduzierbarkeit, Effektvergleiche und Vorhersagegüte auf einen Blick. Der codierte Koeffizienten Plot zeigt den nichtlinearen Effekt der Rührgeschwindigkeit und die signifikante Wechselwirkung mit der Temperatur. (SW :Modde)
- Main Effects Plot mit Vertrauensintervallen:
Heinz erstellt zusätzlich sogenannte Haupteffekt-Plots, in denen er den Einfluss jedes Faktors auf die Zielgrößen isoliert darstellt – jeweils ergänzt durch den Vertrauenskorridor.
So kann er nicht nur erkennen, wie sich Temperatur und Rührgeschwindigkeit grundsätzlich auswirken – sondern auch, welche Streuung (Rauchen oder Unsicherheit) zu erwarten ist, wenn er einen bestimmten Punkt im Designraum wählt.
Und die Ergebnisse?
Sie bestätigen genau das, was Heinz ‘es Bauchgefühl schon geahnt hatte:
- Temperatur: wirkt linear. Höhere Temperatur reduziert die Viskosität, verbessert damit das Benetzen und die Verarbeitung.
- Rührgeschwindigkeit: wirkt nichtlinear. Bis etwa 800 U/min verbessert sich die Festigkeit – danach sinkt sie signifikant. Eine Folge übermäßiger Scherung und Zerstörung der Aerosil-Struktur.
- Wechselwirkung: Besonders kritisch: Bei hoher Temperatur wird der negative Effekt zu hohen Drehzahlen noch verstärkt. Die Stabilität scheint zu kippen – das Füllmaterial wird geschädigt.
Statistische Absicherung durch Regressionsanalyse und t-Tests
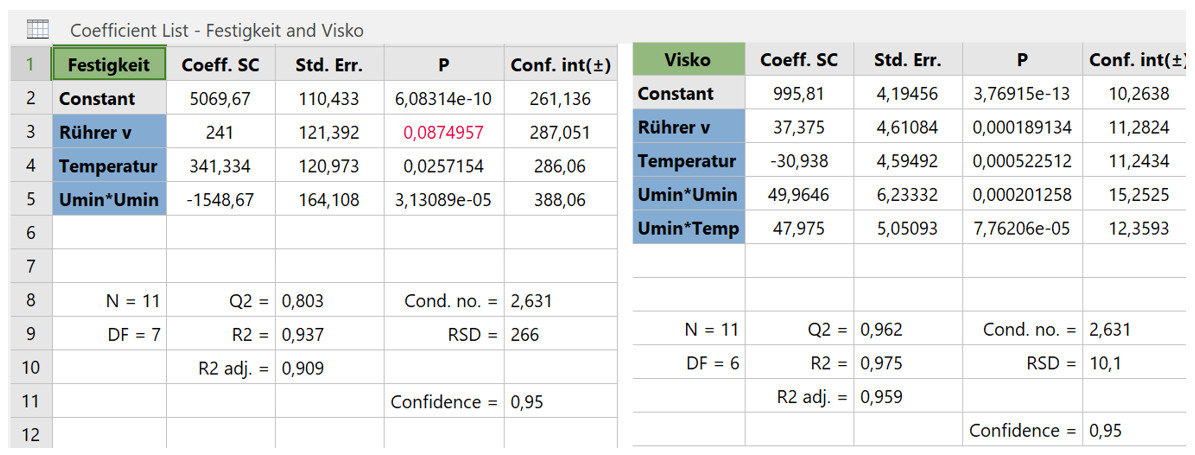
Abbildung 7: T-Test-Ergebnisse aus dem Regressionsmodell. Signifikante Haupteffekte, Wechselwirkungen und Nichtlinearitäten für Festigkeit und Viskosität – codiert, vergleichbar, validiert mit SW Modde.
Am Ende liefert die Regressionsanalyse mit ANOVA die statistische Absicherung dessen, was sich in den Plots bereits angedeutet hat – inklusive der t-Tests, mit denen einzelne Effekte geprüft werden, was sich in den Plots bereits angedeutet hat:
- Der Haupteffekt der Rührgeschwindigkeit ist signifikant – sie beeinflusst z. B. die Viskosität direkt.
- Die Wechselwirkung zwischen Temperatur und Rührgeschwindigkeit ist ebenfalls signifikant – vor allem bei der Festigkeit wird deutlich: Je nach Kombination wirkt Temperatur verstärkend oder kompensierend.
Und besonders wichtig: Der Effekt der Rührgeschwindigkeit zeigt einen Knick: Erst steigt die Festigkeit, dann fällt sie wieder – das ist der typische Verlauf eines nichtlinearen Zusammenhangs. Statistisch belegt durch den quadratischen Term im Modell.
- In Rot dargestellt ist die Rührgeschwindigkeit als linearer Koeffizient. Dieser erscheint zwar nicht signifikant, wird jedoch benötigt, um den nichtlinearen Einfluss der Rührgeschwindigkeit korrekt abbilden zu können.
Und was testet nun der der T-Test im DoE-Kontext?
Was viele nicht wissen: Auch im DoE-Kontext spielen t-Tests eine Rolle – allerdings nicht im klassischen Sinn (z. B. A vs. B), sondern zur Prüfung einzelner Effekte im Regressionsmodell. Im Gegensatz zu klassischen Mittelwertvergleichen (z. B. A vs. B) prüft der T-Test hier, ob ein bestimmter Effekt im Modell signifikant ungleich Null ist – also:
- Ob die Veränderung eines Faktors systematisch eine Auswirkung auf die Zielgröße hat,
- Oder ob der beobachtete Effekt auch rein zufällig entstanden sein könnte (z. B. durch Messrauschen).
Basis dafür ist das Regressionsmodell, das aus der codierten Matrix (z. B. Rührer auf allen Leveln -1,0,1) erzeugt wurde. Für jeden Effekt (z. B. Temperatur, Interaktion, Nichtlineraität) wird ein Koeffizient geschätzt – und dessen Verlässlichkeit statistisch bewertet:
- p-Wert < 0,05 → signifikant = hoher Einfluss mit hoher Sicherheit
- Konfidenzintervall → Aussagebereich des Effekts
- Standardfehler → Maß für Unsicherheit im Modell
In MODDE (und anderen Statistiktools) wird dies automatisch berechnet. Die t-Tests innerhalb der Regressionsanalyse helfen, aus Korrelationen belastbare Aussagen über Ursache und Wirkung abzuleiten – zumindest im Rahmen des experimentellen Designs.
Doch noch entscheidender ist die Frage: Wie lässt sich die gewonnene Erkenntnis überzeugend vermitteln – so, dass sie verstanden und akzeptiert wird?
Viel bedeutsamer als der reine Zahlenwert ist, wie sich das Ergebnis oder der Zusammenhang so visualisieren lässt, dass er klar und nachvollziehbar präsentiert werden kann – idealerweise so, dass offene Fragen direkt im Gespräch am Plot selbst geklärt werden können.
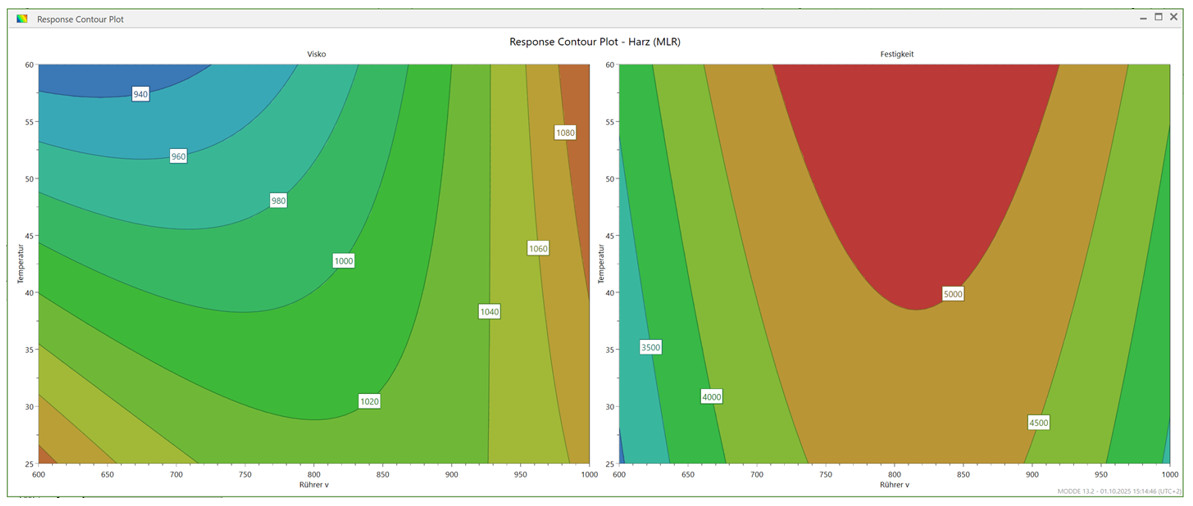
Abbildung 8: Konturplot als Ergebnis des statistischen Modells. Die Signifikanz aus dem T-Test wird hier greifbar, insbesondere die durch t-Tests bestätigten Effekte – rote Zonen stehen für hohe Zielerfüllung, blaue für kritische Bereiche.
Eine Möglichkeit bietet z. B. der Konturplot:
Die Schattierungen repräsentieren das Level der Zielgröße – in unserem Fall z. B.:
- Rot = hohe Festigkeit
- Blau = niedrige Festigkeit
Damit lässt sich auf einen Blick erkennen:
- Welche Faktor-Kombinationen zielführend sind,
- Wo Zielkonflikte oder unerwartete Effekte auftreten,
- Und ob es im untersuchten Versuchsraum überhaupt stabile Prozessfenster gibt.
Gerade bei nichtlinearen oder interaktiven Effekten ist diese Darstellung ein mächtiges Werkzeug – denn sie zeigt nicht nur Trends, sondern hilft auch Übergänge und kritische Zonen zu visualisieren.
Ergänzende Plots zur Präsentation der Rahmenbedingungen und Möglichkeiten
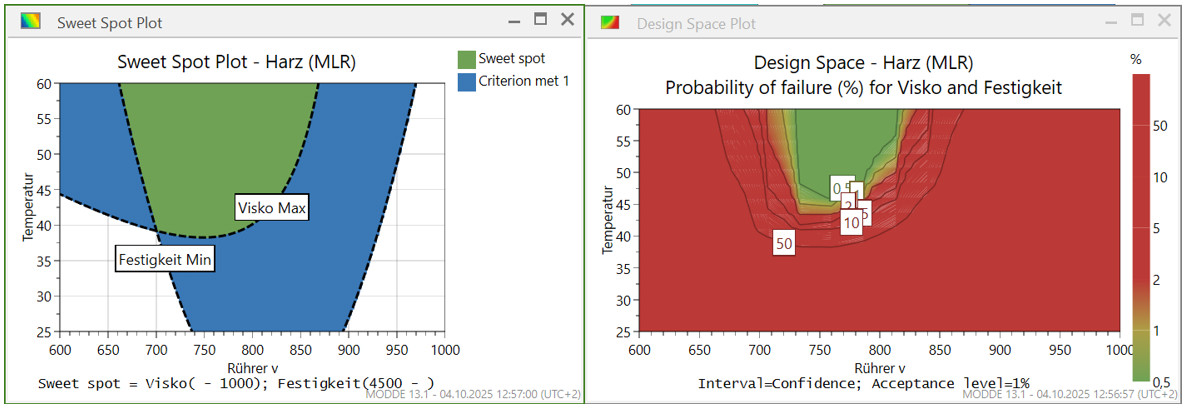
Abbildung 9: Sweet Spot Plot und Design Probarbility Plot erzeugt mit SW: Modde
Das Ergebnis ließe sich auch weiterführend als Sweet Spot Plot oder Wahrscheinlichkeitsplot darstellen. Solche Darstellungen zeigen, in welchem Bereich die Kombination der Faktoren mit hoher Wahrscheinlichkeit zu einem erfolgreichen Ergebnis führt – also zur besten Zielerfüllung bei gleichzeitig minimalem Risiko.
Doch diese Methoden im Detail zu erklären, würde an dieser Stelle den Rahmen sprengen.
Vom Wissen zur Handlung – Die Verbesserungsidee
Jetzt, da die Effekte sauber herausgearbeitet und statistisch abgesichert sind, wird eines klar:
Die Erkenntnisse sind kein Zufallsprodukt, sondern das Ergebnis einer systematisch aufgebauten Versuchsstrategie – von der ersten Hypothese, über die strukturierte Designplanung bis hin zur sauberen Auswertung.
Erst durch dieses methodische Vorgehen konnte Heinz die wesentlichen Einflussgrößen identifizieren, Wechselwirkungen sichtbar machen – und sogar nichtlineare Effekte klar belegen.
Das ermöglicht nicht nur die richtigen Fragen zu stellen – sondern sie auch qualifiziert zu beantworten.
Denn Fragen wie:
„Warum steigt die Viskosität bei hoher Rührleistung plötzlich wieder an?“
wären im OFAT-Vorgehen entweder nie gestellt worden – oder sie wären im diffusen Nebel von Trial-and-Error untergegangen.
Mit dem strukturgebenden Modell dagegen kann Heinz konkret argumentieren, visualisieren und ableiten.
So wird aus einem Bauchgefühl ein echter Erkenntnisprozess – und aus einem losen Problem ein abschließbares Projekt.
Und genau deshalb geht Heinz jetzt den nächsten Schritt – er spricht mit der Technik. Sein Vorschlag:
„Was wäre, wenn wir einen schonenderen Rührer einsetzen – zum Beispiel einen Becher-Rührer mit verbessertem Entlüftungsverhalten?“
Die Idee überzeugt: Weniger Scherung bedeutet weniger Zerstörung der Aerosil-Struktur, eine gleichmäßigere Verteilung der Füllstoffe, weniger Lufteinschlüsse – und damit stabilere Festigkeit und Elastizität, ganz im Sinne der Produktanforderung.
Doch wie immer kommt da noch die Killerfrage, vom Prozessverantwortlichen – Heinz wird schon ganz anders, bleibt aber ruhig. Die Frage lautet:
„Wie erklären Sie sich denn, dass bei hoher Rührleistung die Viskosität wieder ansteigt – obwohl Temperatur doch eigentlich viskositätsmindernd wirkt?“
Eine sportliche Frage. Heinz überlegt kurz – und formuliert eine plausible Hypothese, die er anhand seiner Plots belegen kann:
- Man kann sich die Flocken wie Schneeflocken vorstellen – mit viel Luft drin. Wird zu stark gerührt, zerfallen sie in feine Partikel mit riesiger Oberfläche – das wirkt dann wie ein zäher Brei. Im Konturplot sieht man das deutlich: Die Wirkung hängt fast nur noch von der Rührgeschwindigkeit ab.
- Wird bei moderater Temperatur eingerührt, sinkt die Viskosität – begünstigt durch die erhöhte thermische Bewegung (Brownsche Molekularbewegung), die das Dispergieren unterstützt.
- Bei zu hoher Rührgeschwindigkeit hingegen wird die Primärstruktur zerstört: Die Flocken zerfallen, die effektive Oberfläche steigt stark an – und genau das führt zu einem erneuten Anstieg der Viskosität.
- Das lässt sich auch im Konturplot erkennen: Die Isolinien verlaufen nahezu vertikal – das Verhalten ist damit fast ausschließlich von der Rührgeschwindigkeit abhängig.“
Und Heinz ergänzt noch einen letzten Gedanken – sachlich, ruhig, strukturiert:
- „Sicherlich spielen auch Rührzeit, Rührergeometrie und möglicherweise das Entgasungsverhalten eine Rolle.
- Faktoren, die wir in einem nächsten Schritt gezielt untersuchen können. Denn jetzt wissen wir, wie man es richtig angeht.“
🟩 Ein Moment des Respekts – dann Zustimmung.
Fazit – Warum das Design so wichtig ist
Heinz bringt es auf den Punkt:
„Ohne Design hätte ich herumgeraten. Mit DoE konnte ich die Effekte trennen, Wechselwirkungen sichtbar machen – und sogar die wahre Ursache aufdecken: das ungeeignete Rührorgan.“
Denn ein gutes Design erlaubt:
- die Haupteffekte unabhängig zu identifizieren,
- Wechselwirkungen systematisch zu analysieren,
- Nichtlinearitäten sichtbar zu machen
- und aus Daten echte Erkenntnisse abzuleiten – keine Vermutungen.
Die Regressionsanalyse wirkt wie ein Filter: Sie trennt das Wesentliche vom Zufall – mithilfe von t-Tests, die zeigen, welche Effekte wirklich zählen. Und ein einfacher Bar-plot der standardisierten Effekte zeigt visuell, worauf es wirklich ankommt – und was vernachlässigbar ist.
OFAT vs. DoE – die Gegenüberstellung
| Kriterium | OFAT | DoE |
| Einfachheit | + intuitiv | – Benötigt Planung |
| Zeitaufwand | – Viel Aufwand, wenig Nutzen | + weniger Versuche, mehr Erkenntnis |
| Erkennbare Effekte | – Nur Haupteffekte | + Auch Wechselwirkungen |
| Quadratische Effekte | – nur bedingt | + Designbasiert belegbar |
| Statistik einsetzbar | – Eingeschränkt | + voll einsetzbar |
| Aussagekraft | – Gering | + Hoch |
Heinz hat gelernt:
Gute Versuchsplanung ist kein akademischer Luxus. Sie ist die Voraussetzung, um Prozesse gezielt zu verstehen – und nachhaltig zu verbessern.
„Ich hätte fast den falschen Schluss gezogen. Dank DoE konnte ich zeigen:
Es lag nicht am Material – sondern am Prozess. Und ich konnte sogar sagen, wie man ihn besser macht.“
Sein nächstes Ziel?
Noch tiefer einsteigen – in mehrstufige Designs, robuste Modelle und vor allem: bessere Problemformulierung.
Doch für heute ist klar:
„Wer systematisch plant, erkennt mehr. Und entscheidet besser.“
👉 Gab’s einen Aha-Moment? Dann freue ich mich über ein kurzes Feedback – oder einen Kommentar, wo hat es bei Ihnen Klick gemacht.
Your content goes here. Edit or remove this text inline or in the module Content settings. You can also style every aspect of this content in the module Design settings and even apply custom CSS to this text in the module Advanced settings.

Abbildung 10: Stefan Moser – Logo
Mehr aus Ihren Prozessen rausholen?
Ob DoE-Grundlagen oder Spezialthemen wie Troubleshooting, Screening, Optimierung, Mischungsdesigns oder Robustheit – ich unterstütze Sie mit praxisnahen DoE-Trainings, gezielter Beratung und methodischer Begleitung. Auch bei MVDA, DFSS und QFD bin ich an Ihrer Seite – vom ersten Workshop bis zur robusten Umsetzung.
👉 Schreiben Sie mir: info@stefan-moser.com
Meine Trainings finden Sie hier:
Bleiben Sie experimentierfreudig und neugierig!
Ihr DoE-Trainer Stefan Moser

