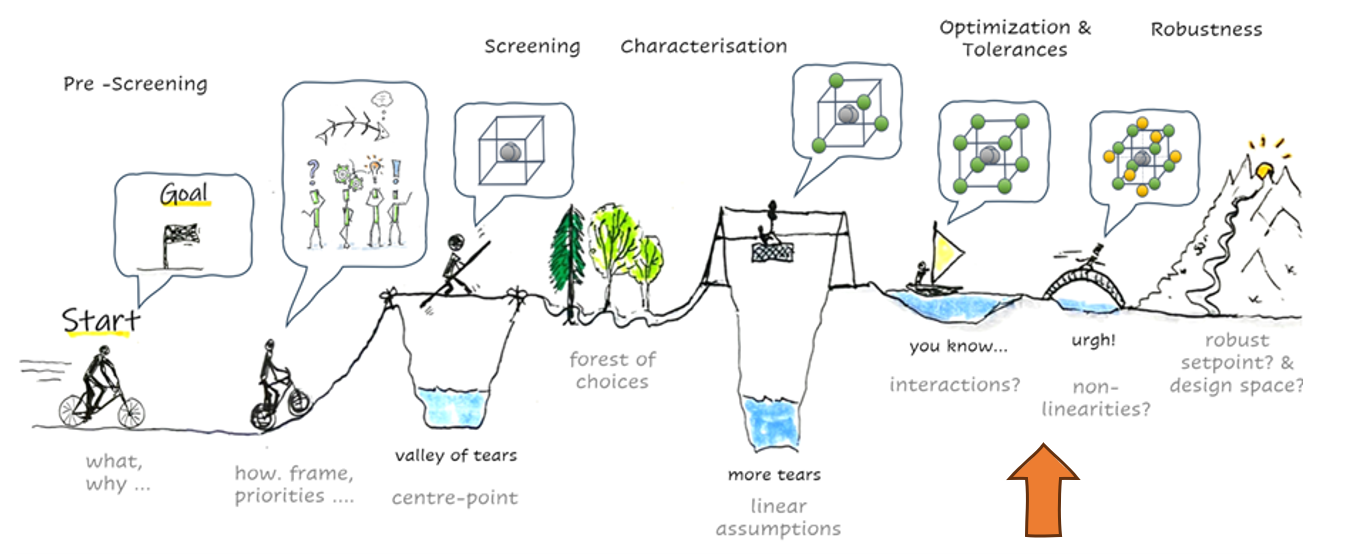
In unserem heutigen Beitrag beschäftigen wir uns mit einem weiteren faszinierenden Bereich des „Design of Experiments“ (DoE): der Optimierung und dem Aspekt der Machbarkeit. Nachdem wir im letzten Teil intensiv die Entwicklung des Modells betrachtet haben, gehen wir nun davon aus, dass dieses Ursache-Wirkungs-Modell uns zur Verfügung steht.

🎯Unser Ziel ist es, mit Hilfe des Modells zu erkunden, ob und wie wir die Ziele, die wir uns vorab gesetzt und hoffentlich gemeinsam priorisiert haben, erreichen können.

Idealerweise wurden diese Ziele im Team festgelegt, was zu einem klaren Ergebnis der Abstimmung führen sollte. Diese könnten beispielsweise sein:

🧭 Ein Multivoting, bei dem die Ziele im Team besprochen wurden.

🧭 Ein bilateraler Vergleich, der aufzeigt, welche Ziele dem Team besonders wichtig sind.

🧭 Ein Pareto-Diagramm, das die Ziele und ihre Prioritäten visuell anschaulich darstellt.

Neben diesen Methoden gibt es weitere umfassende Ansätze wie Benchmarks, SWOT-Analysen, die Eisenhower-Matrix, Ishikawa-Diagramme und den analytisch- hierarchischen Prozess (AHP), um nur einige zu nennen. Auch wenn für eine einfache Gewichtung nicht alle diese Methoden nötig sind, so unterstützen sie uns doch – insbesondere, wenn sie im Team angewandt werden – dabei, uns der Gemeinsamkeiten und Gegensätze unserer Ziele sowie der Vieldeutigkeit unserer Begrifflichkeiten bewusst zu werden. Dies allein kann bereits dazu beitragen, einen Konsens leichter zu finden.

Doch zurück zu unserem Modell, dank dessen können wir nun Techniken nutzen, um die Bereiche zu identifizieren, in denen unsere Ziele gemeinsam – vollständig oder zumindest teilweise – erreichbar sind. Für eine erste Übersicht sind Konturdiagramme hilfreich, um eine erste Orientierung zu erhalten.

Als Beispiel für die folgenden Diagramme habe ich ein Projekt eines Kollegen gewählt, der mit seinen Kindern das „Popcorn-machen“ optimiert hat. Ihre Ziele waren dabei, den Geschmack (auf einer Skala von 1-15) zu maximieren (>=12) und gleichzeitig die Anzahl der Maiskörner (<=30) zu minimieren.

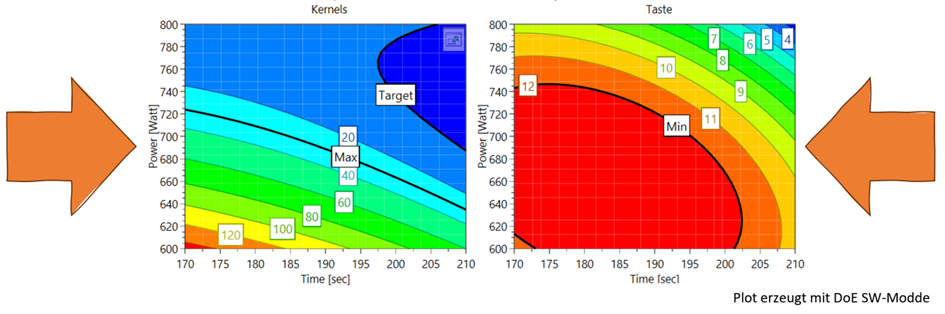
In unserem Beispiel beschränken wir uns aus Gründen der Nachvollziehbarkeit nur auf zwei Zielgrößen und zwei Faktoren (die „Verweilzeit“ in, und die „Leistung“ der Mikrowelle), um das Beispiel übersichtlich zu gestalten. In den meisten DoE-Studien gibt es jedoch deutlich mehr Faktoren und Zielgrößen. Es kann somit herausfordernder sein, Einstellungen zu finden, die die vorab definierten Ziele unter Berücksichtigung der Faktoren erreichen.

Idealerweise können die Diagramme übereinander geschoben werden, wie durch die voranstehenden Pfeile angedeutet, um gemeinsame Zielbereiche zu identifizieren. Vielleicht kennen Sie bereits Begriffe wie Mengenlehre, Venn-Diagramm oder Sweet-Spot-Diagramm.

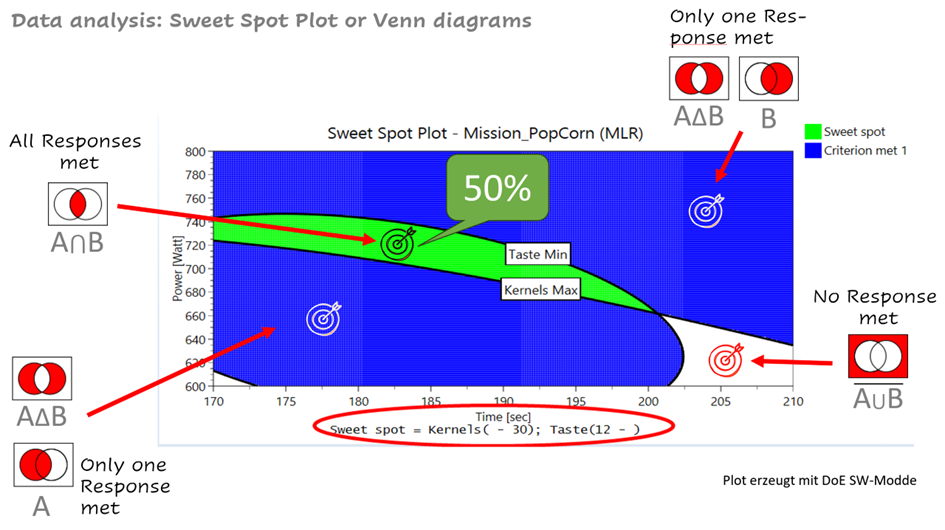
Auf diese Weise kann schnell und übersichtlich dargestellt werden, wo und welche Ziele erreichbar sind. Abhängig von der Anzahl der Ziele werden verschiedene Farben verwendet, die die Erreichung bestimmter Ziele repräsentieren. In unserem Fall sind dies der Geschmack und die Anzahl der Mais-Körner:

🔎 Wird keines der Ziele erreicht, wird der Bereich weiß dargestellt.

🔎 Wird eines der beiden Ziele erreicht, wird dieser Bereich blau dargestellt.

🔎 Werden alle Ziele gemeinsam erreicht, wird der Bereich grün dargestellt.

Die Herausforderung besteht darin, dass die meisten Zielgrößen von verschiedenen Faktoren beeinflusst werden, die wiederum in unterschiedlichem Maße beteiligt sind. Hinzu kommt die unterschiedliche Qualität der Modelle, mit denen jede Zielgröße modelliert werden kann. Diese „Kompliziertheit“ erschwert es, genaue Grenzen für die Zielbereiche zu definieren. Daher bietet dieser Ansatz eine gute Orientierung, ist aber nicht ausreichend für eine verlässliche Aussage, ob alle Ziele sicher im grünen Bereich liegen. Daher die Andeutung mit 50% Wahrscheinlichkeit.

👉 Um diese Hürde zu überwinden, werden wir uns in den nächsten Beiträgen mit fortgeschrittenen Ansätzen wie der Mehrgrößenoptimierung durch den Simplex-Algorithmus und der genaueren Einschätzung durch Monte-Carlo-Simulationen beschäftigen.

Ich hoffe, ich konnte Ihnen wieder etwas Inspiration und Motivation für DoE mitgeben und freue mich darauf, Sie im nächsten Beitrag wieder zu begrüßen.

Während Sie nun vielleicht Lust auf Popcorn bekommen, lade ich Sie ein, über Ihre eigenen Optimierungsherausforderungen nachzudenken. Wie können Sie die Erkenntnisse aus unserem Beispiel auf Ihre Situation übertragen?

Teilen Sie gerne Ihre Gedanken und Erfahrungen mit mir – gemeinsam können wir den Weg zur Optimierung meistern.

Bis zum nächsten Mal, bleiben Sie neugierig und experimentierfreudig!

Ihr DFSS und DoE Experte,

Stefan Moser

👉 Außerdem lade ich Sie herzlich ein, meine Webseite unter www.stefan-moser.com zu besuchen, dort finden Sie weitere Hinweise und Informationen zu Zertifikats -Einsteiger, -Fortgeschrittenen und -Masterkursen in vielen Formaten als offene, Inhouse- oder auch Online-Kurse.

👉 Falls Sie Interesse an einem kompakten Online DoE Intro Kurs mit Zertifikat haben. So empfehle ich meinen folgenden Kurs.